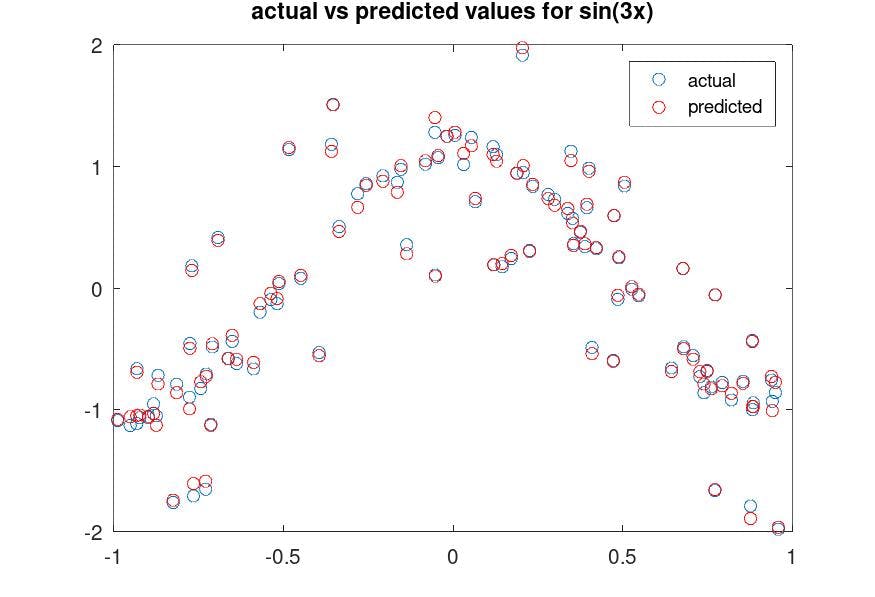
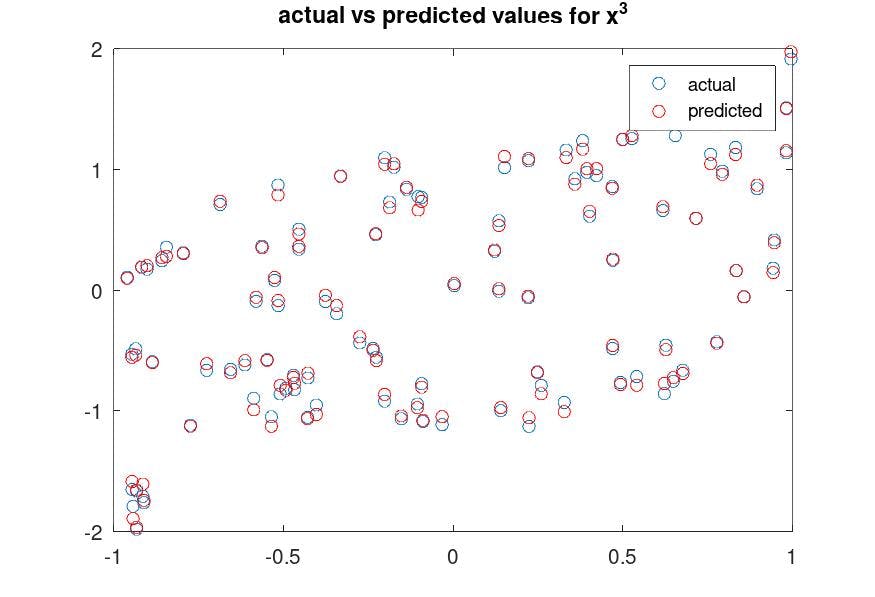
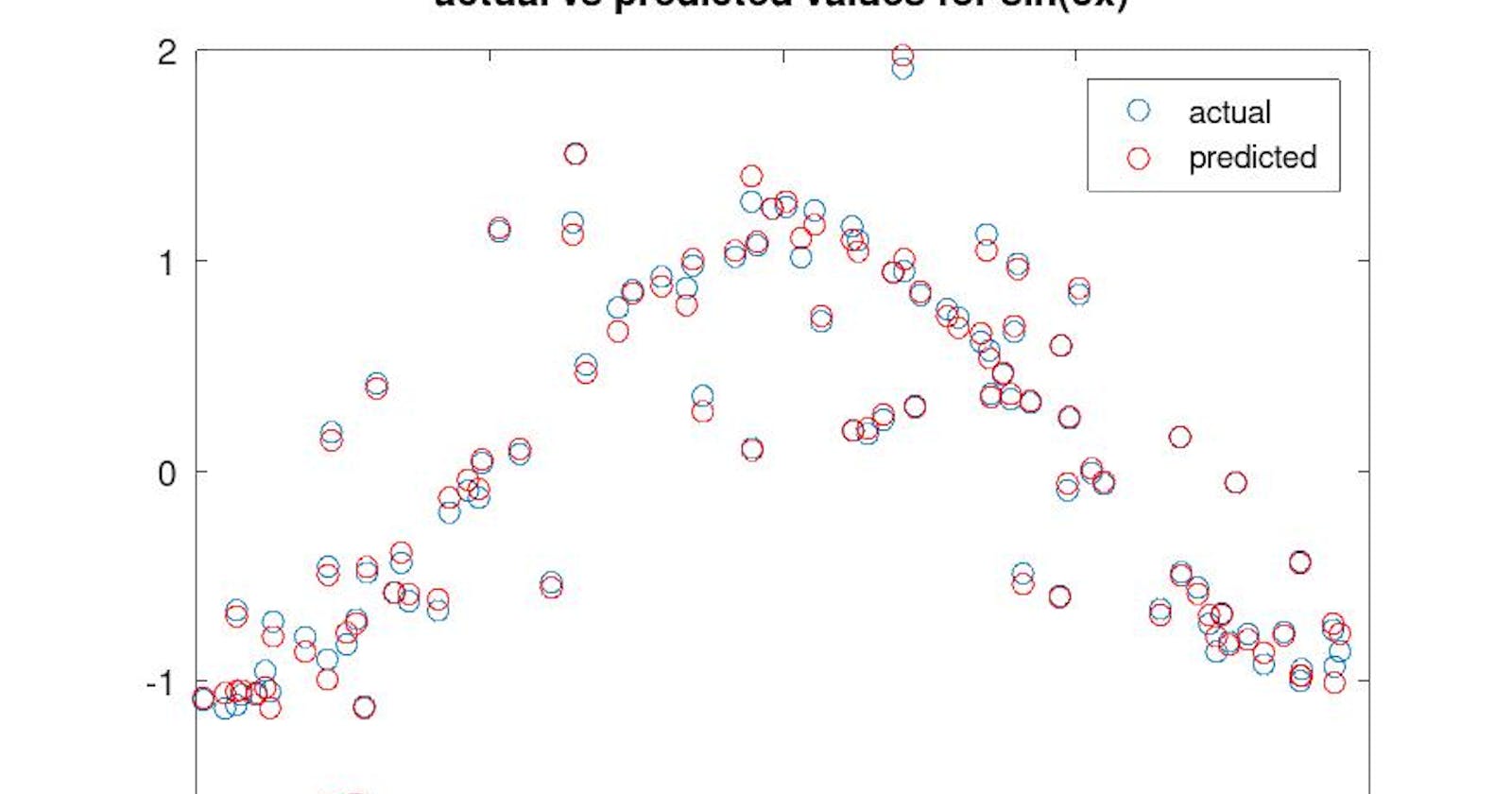
Predicting Values from fitted model
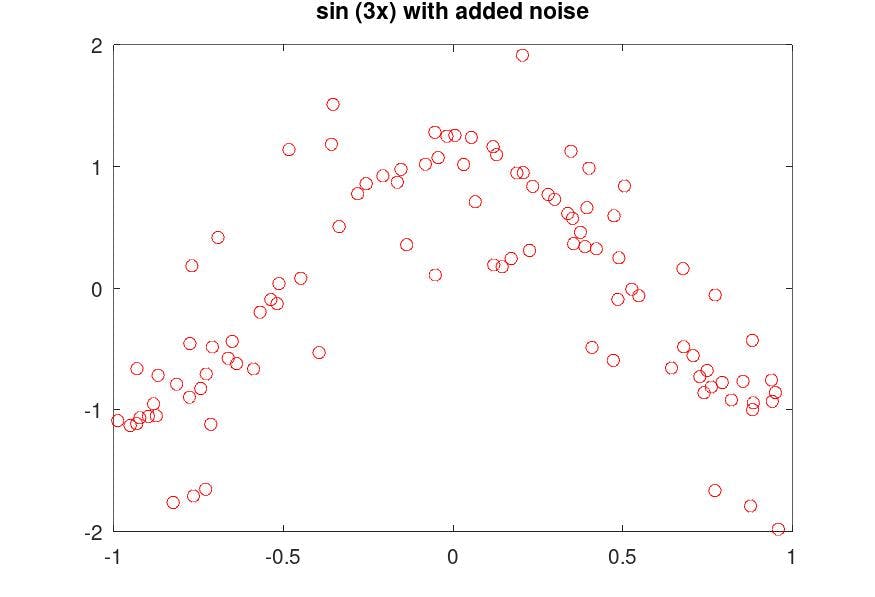
Untill Now we have Fitted the Models for Two different functions for 100 synthetic sample values with added noise.
$$f_1(x) = sin (3x).$$
and
$$f_2(x) = x^3$$
Now when the backfitting algorithm converges, the last returned values from the splinefit function will be the model smooth function. Recall from the last post that the GAM :
$$g(\mu) = b_0 + f(x_1) + f(x_2) + \ldots + f(x_p)$$
where b0 is the mean of the response and f(x1) to f(xp) are the smooth functions. To predict the values we have to implement the link function g(u).
# function predict_val for predicting values
function ypred = predict_val (splstr, X, m)
[n_samples n_features] = size (X);
ypred = ones (rows (X), 1) * m;
for j = 1:n_features
ypred = ypred + ppval (splstr(j), X (:,j));
endfor
endfunction
#perdicting values
y_pred = predict_val (ppf, X, m);
Comparing values