GSoC'23 Week 3: Improving knnsearch and adding kd tree search method to knnsearch

Implementing k-d Tree Search

A k-d tree or 'k' Dimensional Tree, is a special Binary tree in which every node is a 'k' dimensional point. k-d tree search is performed by building a k-d tree for the training data and then performing a search on the k-d tree. Searching in a k-d tree has an average case of O(log n) and a worst case of O(n) which will be an enhancement for searching in large datasets or for a large number of queries.

Let's Quickly take a look at how a K-D tree constructed and searched :

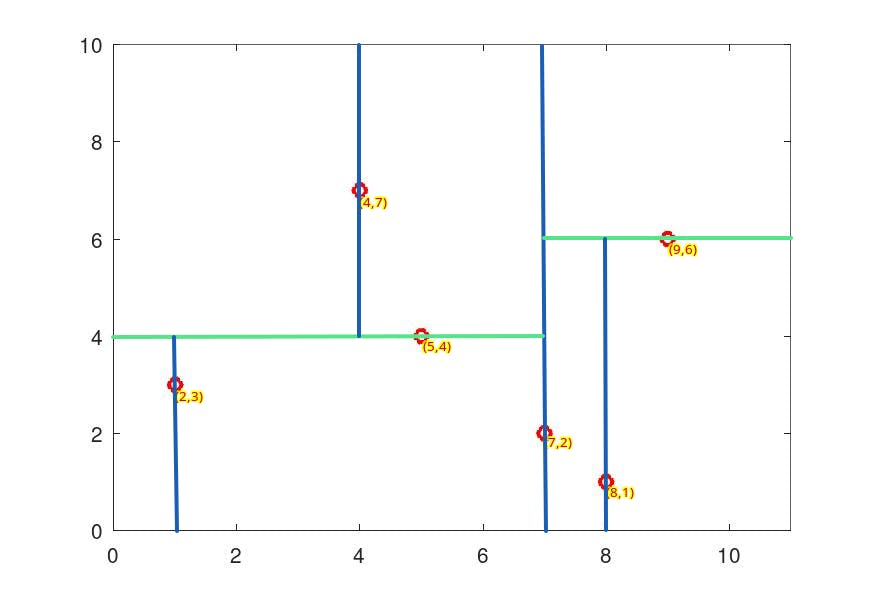
Consider six two-dimensional points : (2,3), (5,4), (9,6), (4,7), (8,1), (7,2)

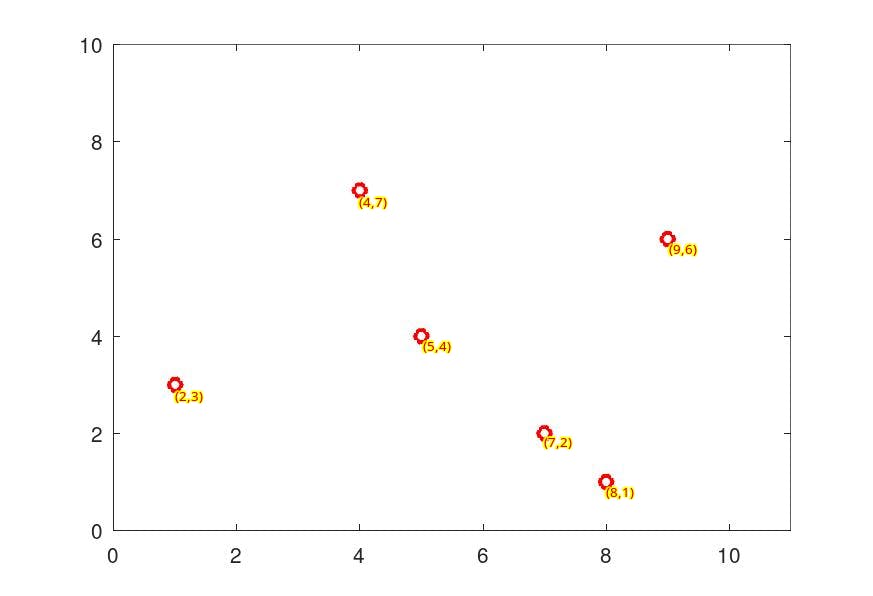
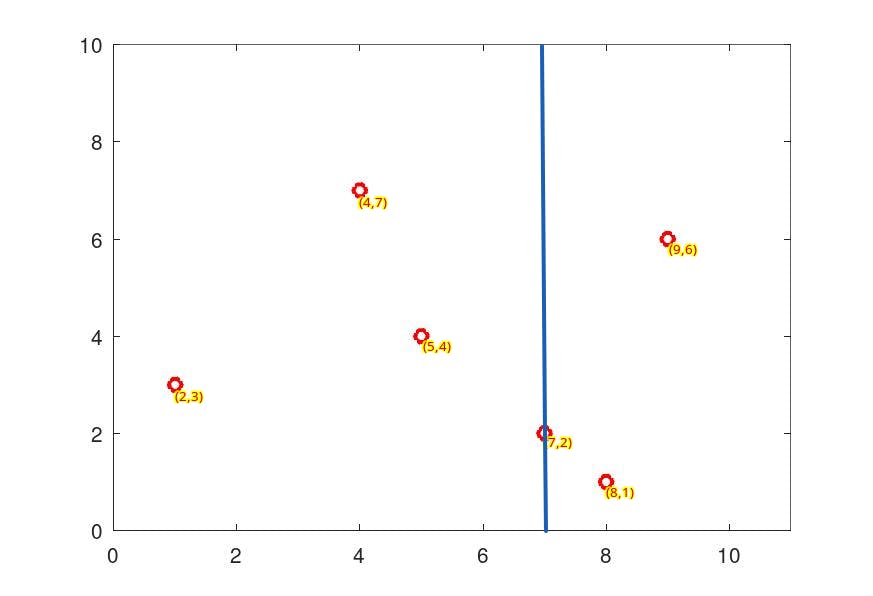
We start with the first dimension sort the data and partition with the middle element. since the median for the first dimension is 7, (7,2) will be the first to insert in the k-d tree and partition the plane into two :

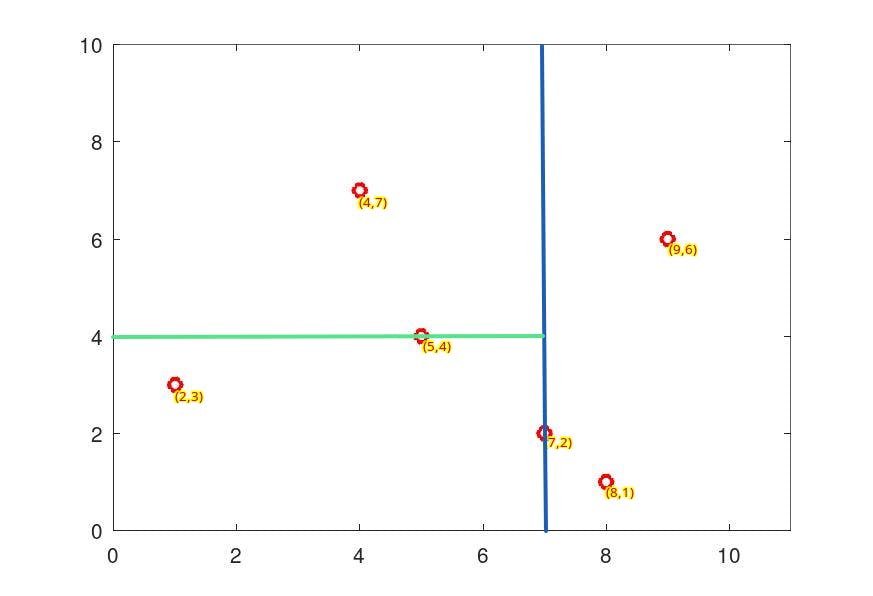
Next cycling the dimensions we have three points (2,3), (5,4), (5,7) for y. sorting we get 5 as the median element :

Now cycling back to the first dimensions and sorting the remaining points we get another partition with (2,3) as the median.

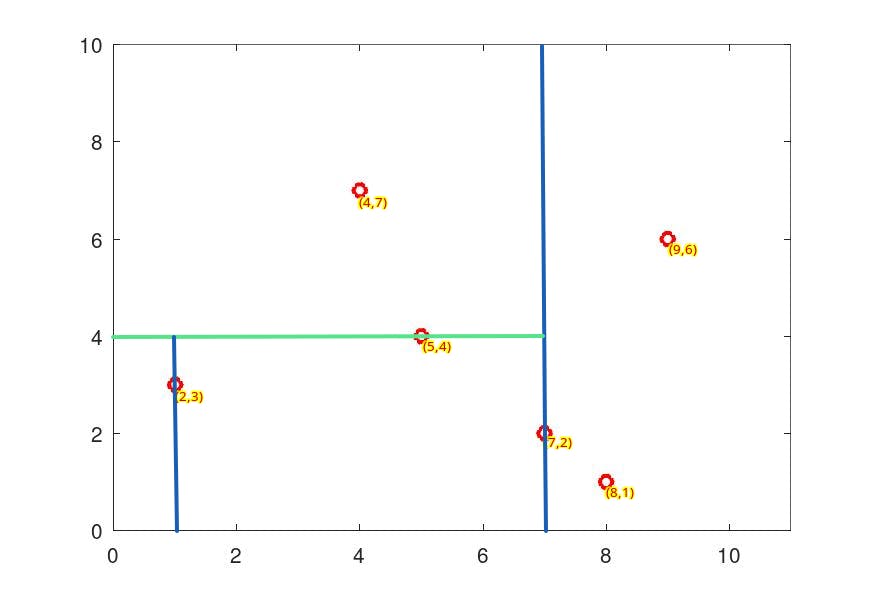
Repeating this process recursively we get the following partition :

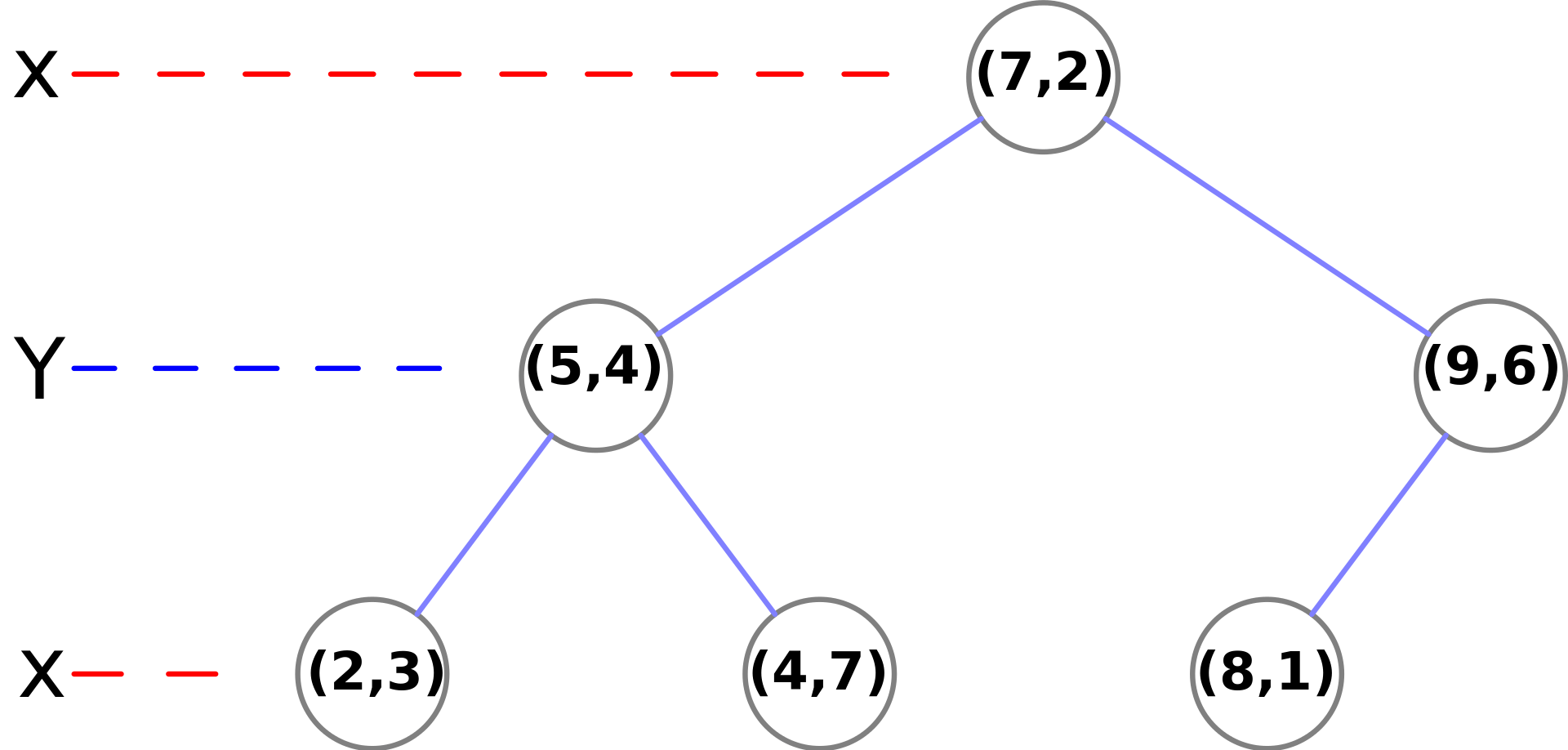
The tree will look like this :

function ret = kdtree_build_recur(x, r, d)
    count = length(r);
    dimen = size(x, 2);
    if (count == 1)
        ret = struct('point', r(1), 'dimen', d);
    else
        mid = ceil(count / 2);
        ret = struct('point', r(mid), 'dimen', d);
        d = mod(d,dimen)+1;
        % Build left sub tree
        if (mid > 1)
            left = r(1:mid-1);
            leftxd = x(left,d);
            [val, leftrr] = sort(leftxd);
            leftr = left(leftrr);
            ret.left = kdtree_build_recur(x, leftr, d);
        end
        % Build right sub tree
        if (count > mid)
            right = r(mid+1:count);
            rightxd = x(right,d);
            [val, rightrr] = sort(rightxd);
            rightr = right(rightrr);
            ret.right = kdtree_build_recur(x, rightr, d);
        end
    end
end

function ret = kdtree_build(x)
    [val, r] = sort(x(:,1));
    ret = struct('data',x,'root', kdtree_build_recur(x,r,1));
end

K-d Tree Search

After constructing the KD-Tree, we initiate the process of searching for the nearest neighbor of a specific point using the following steps:

1. Starting from the root node, the algorithm proceeds down the tree recursively. It follows the same path it would if the search point were being inserted into the tree. The decision to move left or right is based on whether the point is lesser or greater than the current node in the split dimension.

2. Upon reaching a leaf node, the point in that node is saved as the "current best" candidate.

3. The algorithm then unwinds the recursion of the tree. If the current node is closer than the current best, it updates the current best.

4. The algorithm also considers the possibility of points on the other side of the splitting plane that might be closer to the search point than the current best. This is evaluated by intersecting the splitting hyperplane with a hypersphere around the search point, with a radius equal to the current nearest distance.

5. If the hypersphere intersects the plane, it indicates potential closer points on the other side of the plane. In this case, the algorithm traverses down the other branch of the tree from the current node, continuing the recursive process to search for closer points.

6. If the hypersphere does not intersect the splitting plane, the algorithm progresses up the tree, discarding the entire branch on the other side of that node.

7. The search process concludes when the algorithm reaches the root node.

function ret = kdtree_find_recur(x, node, p, ret, k)
    point = node.point;
    d = node.dimen;
    distn = dist(x(point,:), p);

    % Search in the left subtree if necessary
    if (x(point,d) > p(d))
        if (isfield(node, 'left'))
            ret = kdtree_find_recur(x, node.left, p, ret, k);
        end

        % Add current point if necessary
        if (length(ret) <= k || distn <= dist(x(ret(k),:), p))
            ret = kdtree_cand_insert(x, p, ret, k, point);
            #k = length(ret);
        end

        % Search in the right subtree if necessary
        if (isfield(node, 'right') && p(d) + dist(x(ret(k),:), p) >= x(point,d))
            ret = kdtree_find_recur(x, node.right, p, ret, k);
        end
    else
        % Search in the right subtree if necessary
        if (isfield(node, 'right'))
            ret = kdtree_find_recur(x, node.right, p, ret, k);
        end

        % Add current point if necessary
        if (length(ret) <= k || distn <= dist(x(ret(k),:), p))
            ret = kdtree_cand_insert(x, p, ret, k, point);
            #k = length(ret);
        end

        % Search in the left subtree if necessary
        if (isfield(node, 'left') && p(d) - dist(x(ret(k),:), p) <= x(point,d))
            ret = kdtree_find_recur(x, node.left, p, ret, k);
        end
    end
end



function neighbours = kdtree_find(tree, p, k)
    x = tree.data;
    root = tree.root;
    neighbours = kdtree_find_recur(x, root, p, [], k);
end

Adding includeties and sortindices flag to knnsearch

includeties The flag would be given by the user to indicate whether to include the results of knnsearch with tied distances. Let's say you want to search the nearest 3 points to (0,0) and you have 5 points (1, 1), (2, 1), (3, 3), (-3, 3), and (3, -3). Now here if the includeties flag is set true the knnsearch will return all 5 points and if set false Then only the first 3.

sortindices flag is to indicate if the results returned are to be sorted by the distance

Link to PR : [ Link ]